Appendix 4. Modelneuron
The model neuron involves three state variables that include transmembrane potential (U),
a potassium current (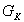 ) and the neuronal output (S). The evolution of a neuron's
state is described by the following coupled differential equations ) and the neuronal output (S). The evolution of a neuron's
state is described by the following coupled differential equations
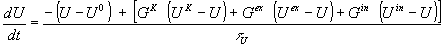 (1) (1)
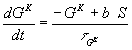 (2) (2)
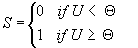 (3) (3)
in which 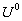 and and 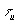 (5 ms) are the
transmembrane resting potential and time constant respectively. Excitatory ( (5 ms) are the
transmembrane resting potential and time constant respectively. Excitatory (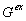 ) or inhibitory
( ) or inhibitory
(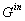 ) input drives the potential towards the respective ionic equilibrium values ) input drives the potential towards the respective ionic equilibrium values
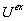 and and 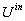 . .
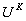 is the equilibrium potential of the potassium conductance
is the equilibrium potential of the potassium conductance 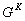 , the evolution of which is
governed by Equation (2). When an output event S occurs, the potassium conductance rises abruptly by a given amount b
for excitatory and inhibitory cells respectively), and then decays exponentially with time constant , the evolution of which is
governed by Equation (2). When an output event S occurs, the potassium conductance rises abruptly by a given amount b
for excitatory and inhibitory cells respectively), and then decays exponentially with time constant 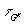 .
The potassium conductance parameters are chosen such that the firing rate of inhibitory cells is higher than that of the excitatory ones.
Equation (3) is a conventional threshold rule. Unlike in the MacGregor model neuron [ref. MacGregor], we used a fixed threshold value .
The potassium conductance parameters are chosen such that the firing rate of inhibitory cells is higher than that of the excitatory ones.
Equation (3) is a conventional threshold rule. Unlike in the MacGregor model neuron [ref. MacGregor], we used a fixed threshold value
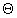 . The values of the equilibrium potentials, the resting potential and the threshold, may be
linearly transformed to physiological values ( . The values of the equilibrium potentials, the resting potential and the threshold, may be
linearly transformed to physiological values (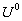 = 0 º -75 mV; = 0 º -75 mV;
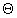 =1 º -60 mV; =1 º -60 mV; 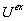 = 7
º 30 mV; = 7
º 30 mV; 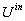 = -1 º -90 mV ; = -1 º -90 mV ;
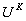 =-1 º -90 mV; b = 12 and =-1 º -90 mV; b = 12 and 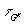 = 15 ms
for pyramidal cells; b = 5 and = 15 ms
for pyramidal cells; b = 5 and 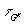 = 7.5 ms for stellate cells). The conductances of pyramidal cells
are = 7.5 ms for stellate cells). The conductances of pyramidal cells
are
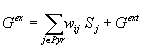 (4) (4)
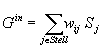 (5) (5)
in which the excitatory conductance 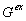 is the sum of synaptic inputs from connected pyramidal cell
and an external input conductance is the sum of synaptic inputs from connected pyramidal cell
and an external input conductance 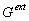 , given by a stochastic spike train with probability of spike event , given by a stochastic spike train with probability of spike event
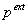 (0.075, with one time of 1 ms) and a strength (0.075, with one time of 1 ms) and a strength 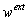 (0.4
(0.4 ). The inhibitory conductance ). The inhibitory conductance 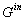 is the weighted sum of
synaptic inputs from connected stellate cells. is the weighted sum of
synaptic inputs from connected stellate cells.
Uit: Murre, JMJ & Raffone, A. (in prep.). Synfire chains. Manuscript in preparation
| 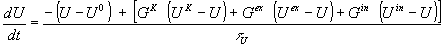 (1)
(1)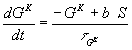 (2)
(2)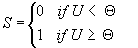 (3)
(3)