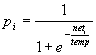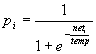Appendix 2. How the TraceLink paradigm works.

Introduction

TraceLink is a connectionist paradigm introduced in the papers of Murre and Meeter on the TraceLink model of amnesia (Murre, 1996; Murre & Meeter, subm.). The last section, from Murre and Meeter (subm.) and for afficionados only, explains in detail the working of this paradigm. The first two sections focus on how TraceLink is implemented in Nutshell, and gives only a cursory explanation of the paradigm itself.

The paradigm uses Hebbian learning, and a simple linear integration of inputs. The two distinguishing features of the model are the fact that nodes fire stochastically, and the soft k-Winner-Take-All character of layers in TraceLink networks.

The likelihood with which a node fires is a function of the balance of inhibition and excitation: if a node receives more excitation than inhibition, the likelihood is greater than 0.5, and it is smaller than 0.5 if inhibition dominates excitation. Excitation is the sum of inputs from the other nodes in the network, inhibition is a variable, equal for all nodes in a layer, whose composition will be explained later. The degree of randomness is controlled by the 'temperature' parameter. If the temperature is high (e.g., 1), then the nodes fire in a very random way, and the difference between excitation and inhibition must be large to have an impact on the node. If the temperature is low (e.g., 0.1), small differences between excitation and inhibition are enough to result in a very high, or alternatively very low, likelihood of firing.

TraceLink implements a soft k-Winner-Take-All firing regime. Inhibition is regulated in such a way that the fraction of nodes that fires in a given layer is kept as close as possible to the fraction k given by the user. If a fraction bigger than k of the nodes fire, then inhibition is raised so that less nodes will be able to fire in the next iteration. If a fraction smaller than k of the nodes fires, then inhibition is lowered so that more nodes will be able to fire. This process will continue until the fraction of firing nodes reaches a stable state of around k (this process of settling can take between 20 and 200 iterations).

Inhibition is the sum of two amounts: fast inhibition (T) and slow inhibition (tau). Fast inhibition is adjusted, as a name suggests, more rapidly than slow inhibition. Both, however, are adjusted with the objective of bringing the fraction of nodes that is active close to k.

Parameters of the TraceLink paradigm in Nutshell

On the node level

A node has four parameters: 'Act', 'Net', 'Clamped' and 'Deactivated'. 'Act' stands for 'Activation', and can have the values 1 (active, fires) or 0 (inactive). 'Net' is the sum of excitatory inputs that the node received in the last iteration. A node is 'Clamped' if its activity state is not updated, i.e. the node stays in a its activity state independent of the input it might receive. A 'Deactivated' node is lesioned; it does not function anymore.

On the tract and connection level

A connection between two nodes has only one parameter: its 'weight'. This parameter has the standard connectionist interpretation. Tracts are objects that contain all the connections from all the nodes in one layer to all the nodes in another layer (or all the other nodes in the same layer). They have five parameters. 'MuPos' is the positive learning constant, i.e. how much is added to the weight if both the sending and the receiving nodes are active. 'MuNeg' is the negative learning constant, the constant associated with the LTD-component of Hebbian learning. If the sending node is active and the receiving node is not, then 'MuNeg' is subtracted from the weight. 'P Creation' is the likelihood that two nodes that are not connected get connected if both are active in a given iteration. Connections are assumed to not exist if the weight on the connection is equal to 0. 'P Creation' is thus the likelihood that a weight of 0 will rise to a positive value if Hebbian learning requires that the connection learn. 'WeightMax' is the maximum value that a weight in the tract can attain. If 'WeightMax' is for example equal to 1, weights will not become higher than 1 (the minimum value a weight can have is always equal to 0). 'Dampening' is a factor with which all weights in the tract are multiplied at the moment that inputs are calculated. Setting 'Dampening' at a higher or lower level than 1 allows for weights to be modulated temporarily up- or downwards.

On the layer level

Layers instantiate many parameters. 'Width' and 'Height' are the layer widths and heights. 'Active Nodes' is the nomber of nodes in the layer that is active (actually, this is a moving average over the last iterations - with always 1/2^nd determined by the last iteration, 1/4^th by the iteration before that etc.). These three parameters cannot be changed. Other parameters can be changed by the user.

'Inhibition T' and 'Inhibition tau' implement fast and slow inhibition respectively (note that these are separate for every layer). Their magnitude depends on the size of the layer and on the magnitudes of the excitatory weights. Often magnitudes are around 0.05 for 'T' and 0.9 for 'tau'. 'K' is the number of nodes in the layer that should be active. Inhibition is adjusted at every iteration to bring 'Active Nodes' closer to 'K'. 'Temperature' determines the degree of randomness in the layer.

On the workspace level

On the workspace level (in the browser: parameters under 'general' when one clicks with the right muse button), there is only one parameter: 'Cycle Steps'. 'Cycle Steps' is the number of iterations that the model runs if you use the 'Act Cycle' method. If you intend to run many iterations, it might be more efficient to adjust this parameter than to push or call the 'Act Cycle' method n times.

Methods of the TraceLink paradigm in Nutshell

Part 2: Details of TraceLink nodes

The model is based on binary, stochastic nodes that fire synchronously. The firing thresholds of the nodes in a module are controlled by a 'threshold control' mechanism: inhibition in a module is diminished if there are not enough activated nodes (i.e., less than some target number k) and increased if there are too many. At each iteration, after all node activations have been updated, a learning rule is applied to all connections. The details of these mechanisms are as follows:

Activation rule

A node i has an activation a_i that can take on either of two values: 0 or 1. The probability that node i will 'fire' (i.e., that its activation becomes 1) increases with its net input, as follows:

where net_i is the total input activation to node i:

net_i= weighted input activation - inhibition

The weighted input activation can be written as:

where w_ij is the connection weight from node j to node i, a_j is the activation value of node j, and n is the number of nodes in the model (if there is no connection between j and i, w_ij is zero by default). Inhibition is discussed in the next paragraph.

The temperature parameter temp in Eq.1 controls the degree of randomness of the nodes: if temp is near zero the nodes behave as simple threshold devices, if temp is very high the role of the net input is very limited and the node will take on values 0 or 1 randomly. We used a temperature of 0.2 in all simulations.

Threshold control

The total number of activated nodes in a module (called A) is constantly monitored and firing thresholds are adjusted to ensure that this number does not wander too far from the target number k, Each module can have a different k and inhibition control in a module is independent of that in other modules. We assume that one of the functions of inhibition in the brain is to keep the level of activation (i.e., the average number of activated neurons) in a certain region constant. Furthermore, we assume that the total number of activated neurons, k, is relatively low (cf. Abeles, Vaadia, & Bergman, 1990). The effect of the inhibitory system is thus to keep the number of activated nodes A as close as possible to the target number k.

The system achieves this by constantly adjusting two thresholds T and t . Inhibition is the sum of the fast changing threshold T multiplied by the number of active nodes A, and the slow moving threshold t :

inhibition = TA + t

We believe that T reflects the activation of the basket cells and that it is able to change relatively quickly. In addition to the action of inhibitory cells, we assume that there are also slower working processes. These may reflect synaptic changes and growth processes. 'Slow' inhibition is modelled by the threshold t .

The control of fast inhibition, T, is straightforward: If the total activation at time t (A_t) is higher than k, T is increased (more inhibition), if A_t is lower it is decreased. In particular, if A_t is much larger than k, T is increased a lot; if A_t is only a bit larger, T is increased a little. A very simple implementation of the approach is used here:

If A is much (i.e., more than a crit proportion) larger or smaller than k:

if A_t > (1+crit)k

T = T + D _t

if A_t < (1-crit)k

T = T - D _t

else, if A is only a little bit larger or smaller than k:

if A_t > k

T = T + 1/3 D _t

if A_t < k

T = T - 1/3 D _t

where crit is the criterion for deciding whether A_t is much larger or smaller, and D _t is the change made to T (crit = 0.20, and D _t = 0.01 works well for the simulations reported here). One disadvantage of this method is that T may change too quickly so that the module starts to oscillate violently. To prevent this, A_t is dampened by making it a moving average of the current activation and the activation of previous iterations. When A*_t is the current level of activation, the value used to compute both the level of inhibition A_tT and the change in the parameter T is:

A_t = 0.5A_t-1 + 0.5A*_t

This precedes calculation of the new threshold T.

The slow inhibition process aims to keep the 'slow threshold' t equal to TA. When the equilibrium is disturbed, for example, if the activation is diminished due to a lesion, t slowly decreases to a new equilibrium value. The speed of this change is determined by the parameter D t . Because we envision the adjustment to be slow, D t is chosen low (0.001). The expression for calculating t _t+1 at t+1 is

t _t+1 = (1-D t )t _t + D t TA

The amount of 'fast' inhibition is bounded by a minimum value T^min and a maximum value T^max. If T < T^min it is set to T^min, and if T > T^max it is set to T^max. Similarly, t is also kept between upper and lower bounds: if t < t ^min, t is t ^min; if t > t ^max, t is t ^max. T^min and t ^mi were set to 0. T^max and t ^max were set to such high values that they were never reached in the simulations.

Learning rule

The learning rule is a simple Hebbian rule that also allows decreases in weight, as follows:

D w_ij = m ⁺ a_ia_j - m ^- a_i (1 - a_j)

and

w_ij(t+1) = w_ij(t) + D w_ij

where D w_ij represents the weight change and m ^- and m ⁺ represent the learning rates. Both m ^- and m ⁺ must be larger than 0. The weights are kept within the interval [0,1] by setting w_ij=1 if w_ij >1, and w_ij =0 if w_ij <0.

Learning rate can vary rapidly -due to certain central states (e.g., motivational)- or slowly, (e.g., due to aging). The effects of learning rate variations are studied in various simulations in this paper, but it is kept constant from one iteration to the next (i.e., it only changes when there is a change in learning phase). In a more general version of the model the learning rate would vary continuously (cf. Murre, 1992).